Asymptotes
Horizontal and vertical Asymptote from a rational expression
A function can have at the most one horizontal asymptote but many vertical asymptotes.(apparently this arises because of the way function is defined-not more than one f(x) value for any given 'x' value.(vertical line test property).A function can have both asymptotes.
Horizontal Aymptote: 'x'approaches + or - infinity but f(x)is generally bounded by the H-asymptote line.[x-horizontal axis, f(x)-vertical axis always]
Horizontal Asymptote.(example asymptote at y=1)
(mathsisfun.com)
(mathsisfun.com)
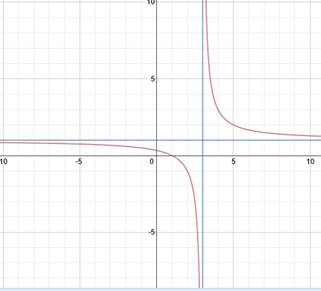
Vertical Asymptote:'f(x)'approaches infinity as x approaches a some value towards the origin .
Vertical Asymtote(example of asumptotes at y=-2,y=2 and x=0)
(study.com)
Vertical Asymtote(example of asumptotes at y=-2,y=2 and x=0)
(study.com)
Video-Finding V.Asymptotes One more video
Squeeze Theorem-Nice graph-
(do not be scared by the graph-its simple once you know)
Squeeze Theorem-Nice graph-
(do not be scared by the graph-its simple once you know)
| Common Functions | Function | Derivative |
|---|---|---|
| Constant | c | 0 |
| Line | x | 1 |
| Constant multiple Reciprocal | ax 1/x | a - 1/x2 |
| Square | x2 | 2x |
| Square Root | √x | (1/2√x) |
| Exponential | ex | ex |
| ax | axln(a) | |
| Logarithms | ln(x) | 1/x |
| loga(x) | 1 / (x ln(a)) | |
| Trigonometry (x is in radians) | sin(x) | cos(x) |
| cos(x) | −sin(x) | |
| tan(x) | sec2(x) | |
| Inverse Trigonometry | sin-1(x) | 1/√(1−x2) |
| cos-1(x) | −1/√(1−x2) | |
| tan-1(x) | 1/(1+x2) | |
| Rules | Function | Derivative |
| Multiplication by constant | cf | cf’ |
| Power Rule | xn | nxn−1 |
| Sum Rule | f + g | f’ + g’ |
| Difference Rule | f - g | f’ − g’ |
| Product Rule | fg | f’ g + f g’ |
| Quotient Rule | f/g | (f’ g − g’ f )/g2 |
| Reciprocal Rule | 1/f | −f’/f2 |
| Chain Rule (as "Composition of Functions") | f º g | (f’ º g) × g’ |
| Chain Rule (using ’ ) | f(g(x)) | f’(g(x))g’(x) |
| Chain Rule (using ddx ) | dydx = dydududx | |