Reiman Sums and def imtegrals Khan

Reiman analysis Khan series 1
Reiman analysis Khan series 2
Reiman Khan Trapezoidal rule 3
Reiman sum and definite integrals
Review Reimann

DOMAIN ANALYSIS

Informal Explanations:

All real values of 'x' - infinity to  + infinity that permits a function to exist.

There are only 3 types functions that restrict domains.

1.Functions under a even root radical, or exponent m/n has n only as even  number.
(ex x^1/2; x^3/4;x^5/4--) have to be >=0

domain restriction graph of fractional exponents
you can experiment in the above link apart from study.

2.Functions that have denominators whose 'x' value will make it '0'.
The function is DNE at the 'x' value.(ex 3x-1/3x-2  cannot have x=2/3  f(2/3) is DNE)
Domain of rational functions

3.log f(x) must have f(x) greater than'0'.
 The term of the log ;That is f(x) must be >0.
Ex: log{ (x^3)-7} must be such x^3-7 >0 (be careful to exclude '0')

It is the same rule for all types of bases.Bear in mind that, Base 0 does exist as it is absurd.

Intermediate Value Theorem

Mean Value  Theorem

Extreme Value Theorem

Rolles Theorem

1.These are informal explanations for quick recollection of its actions.

Conditions:

2.All functions must be differentiable (so it must also be continuous) to apply these theorems in the open interval  specified. (includes end points)

3.The result of the theorem is applied in the  closed interval [a,b] (that is excludes end points)

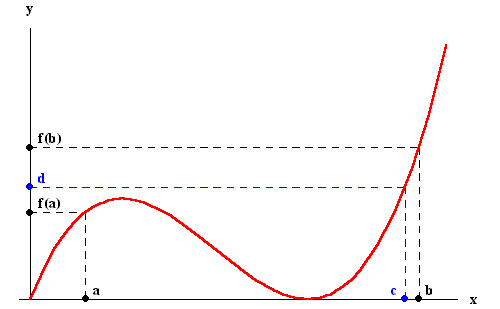
Intermediate Value Theorem:

IVT picture

You can find f(c)=d intermediate between f(a) and f(b)

Mean Value Theorem

For a secant line slope f(b)-f(a)  / (b-a)   you can find at least one  point between 'a' and 'b' where a tangent line is parallel (same slope as secant line) to the secant line .

Rolle Theorem

If f(a)=f(b), then a point 'c' has slope =0 {special case MVT}

Extreme Value Theorem

Between f(a) and f(b) there is a f(c) maximum and f(d) minimum.

Examples of problems:

Here are a few more typical Mean Value Theorem (MVT) problems.  Note that when we get our value of c, we have to make sure it lies in the interval we’re given.

Note also that these problems may be worded something like this:  For what value of c on a certain open interval would the tangent to the graph of a certain function be parallel to the the secant line in that closed interval?

AP problems

MAX MIN CONCAVITY INFLECTION Points

Characteristics of a functions:
max Min point on a graph
Features of a curve of functions Video
Displacement,Velocity acceleration .  school typr problem
Concavity

Answer the following questions based on above :
1.How do you identify the derivative signs at different points on the graph?
2.What features of the slope defines that the curve at a point region is concave down/concave up (cup up/cup down)?
3.What is an inflection point.Where does an inflection point occur in a graph? What is the difference between the slope '0' point (also known as stationary point) and an inflection point.
4.Does the concavity  always alternate like up/down in general or can there be exceptions ?If exceptions are there -them what are they?

Inflection point testing Video tells you some techniques of analysing.
Answer the following.
The video showed a quick way to analyse slopes using signs without drawing the derivative graph.,what was it.Give example.
A note on linkin 1st derivative fraph to f(x)
f '(x) -  to 0 to+ U [smiling f(x) ] ;f'(x) + 0 -  ∩ (Sad f (x))
It also showed how to look for concavity using  signs of 2nd derivative  and the inflection point..describe it.
When can there be no inflection point?
Exercise:
1.Graph the following f(x), fulfilling all conditions:

Domain [-3,3],f(-3)=4,f(3)=1

f(x) increasing on [-3,-1],f(x) decreasing on [-1,1],f’’(x)>0 on [-1,1],f”(x)<0 on [1,3].

Find Abs Max and Min points and inflection points.

State with reasons
2. y=-x^3=3x^2+1 .at which point is the slope Maximum.

 Learning CapsculeBahskara Academy link

Quick Revision:
Limits
1.Quick start
2.Infinite limits graph.
3.Limits from graphs.
4.1.Graphing limits   2.School  exercise

Inequalities-Sign flips

The sign between two expressions or quantities change under certain conditions.The slide show explains it.
slide show

Absolute Value

Limits Graphs Plotting strategy

Watch the slide shaow presentation
Vdeo graphing of limits
Slide show exercises.

New Day 15

Chain Rule Easy

Chain Rule Intermediate

Chain Rule Harder Problems
Implicit functions and its differentiation   Imp.Diffn Ex1   Ex2  Ex3  Ex4  Implicit differentiation

Day 14

You should also memorize (x)'=1;  (√x)' =1/2√ x

Videos on differentiation (same as Day 13- to watch 10~14)

New Day 13

DERIVATIVES USING DEFINITION

Task 1.Watch the slides show and the videos links  in it DERIVATIVES 2 slide show

*Try answer what is the graphical significance of differential quotient and derivative (tangent/secant etc..) ?

*What is the general approach to getting the derivative of a function?

QUICK REVIEW

MEMORIZE DERIVATIVE OF BASIC IMPORTANT FUNCTIONS

f(x) = c,( where c is a constant), xⁿ,  ln x, e^x, sin x and cos x
All  derivatives of a function can be obtained from the below mentioned .

The videos below is an introduction to differentiation rules and how to use them.

Videos on differentiation

Day 12

SLOPE EXERCISES on Derivatives

Slide on derivative curves-understanding

TIP:In the problems below  the idea should be to not get lost in increasing/decreasing shapes of the derivative graph,but to concetrate on the sign of the derivative and how the sign changes...then look for similar slope changes in the matching f(x) graph.

Reminder Trick to avoid confusion:

 Concentrate only on +ve or -ve part   derivative graph .The zero crossing in the f '- graph is the '0' slope point of the f-graph.If you remember this you can identify the related graphs...with some additional checks.

The positive part between two zeros in the f '-graph is the positive slope of the f-graph and vice versa.

You can easily be carried away in a maze when you start analyzing derivative as increasing decreasing slopes-so avoid looking at it the f ' graph (it is mental trick to avoid confusion) though you will be tempted by habit.

More exercises on increasing decreasing

Derivative graphic Tester1(geogebra) Tester2(desmos)

day 11

Derivatives 2

The slide show has some videos to be seen in links in slide 4

Day 10

Limits of trigonometric functions (no proof for now -only memorise)

The property is derived from squeeze theorem (because substitution produces 0/0) Sq Theorem Video Khan

Results

Lim x =>0    ( sin x)/x  =1

Lim x=>0     (1-cos x)/x  = 0

Lim x=>0    (tan x)/x = 1

TIP:  Squeeze theorem  is a useful tool for solving.However you should develop the skill to identify problems (in limits only) where it can be applied.I noticed that when you are given a function (mainly combined with trigonometric) , where   limits of a part of the function are known,then the problem can be manipulated algebraically (by addition,subn, multpln, divn,exp ) and fitted to suit the application of the theorem and limits derived for the function.The blog will not deal with it as it can be done at school...however remember the above limits.

----------------------------------------------------------------------------------------------------------------------------------

We shall be doing problems in derivatives after completing the intro in slides.
Visual Intro to derivatives-slide show

Day 9

Do exercise 1.8 from problem book (given below) after the Khan Video in Day 8

Rate of Change Graphs

Day8

.Horizontal asymptotesVideo

This the application of limits(x approaching +ve or -ve infinity) to find horizontal asymptodes-

No other logical or algebraic method exists.

Vertical asymptotes are very easy to find (x value that makes denominator=0)

Find the Limits- (most problems can be done -using the mental short cut trick)

Answers

Video Vertical asymptotes
Limits -infinity related Khan Videos to do

Day 7

Transformation of graphs google slides by TSK Slide editable
For the next exercise you should learn to use the calculator.Calculator based questions are there in AP Calculus,Its allowed for 45 mts or so...but only some problems will need it.

Day 6

Knowledge accumulation for future use:

Library of Functions Video - a good video on basics of function graphing(-missing exponential and logarithmic function graphs)Useful for SAT, algebra,calculus(integral)

Understand the standard term for the type of function (lke identity,quadratic, cubic,reciprocal etc)

{Video on Library of Functions}

Day 5

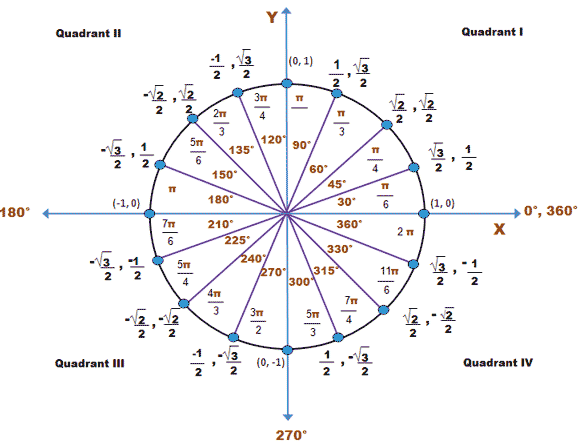
*After completing trigonometry unit circle (downloadded sheet) by filling it and removing errors if you found any.Check why you made the errors.(Remember  sine is I and so cosine is _ (my hand signal) and relate their signs to quadrants .

 +

*Practice range  of square root functions and log functions

Limits at infinity  (x approaching infinity)

Tip:  In  rational expression only the highest power maaters for the rsult at infinity in numerator and denominator.See iff you can do the limits mentally using that idea as a short cut.after watching the videos.

Limits at infinity video1 (with graph);Limits at Infinty Video 2  ;  Limits at infinity video(square root example) Limits at infinity soving tricks Video  Asymptodes and limits

*Down load exercise on limits at infinity from P.Cal and check answers with the solutions

*Do the connected assignment (no answers)
Recollect

What can you recollect and say about (0-0),(0/0),0+0),(-0-0)?What can you say if you replace 0 by infinity in the question?How do you overcome the problem of powers of 'x' when x approaches + or - infinity.?Scribble you answer and keep it ready for a chat.

Exercise quick review of methods learnt.

Day 4

The unit circle for trigonometric ratios 
Notice that there are 3 important angles between π and π/2.They are 30 deg(π/6) , and 60 deg (π/3)45 deg(π/4).The others can be derived by using their location in the quadrant with signs .A litle practice s sufficient .These ratios will appear throughout the college courses in physics and maths and engineering.
Memorising TIP:(Just think why cosines are always negative left of y-axis.Also why sine are negative below the x-axis.)
The easiest ratios are for 45 deg(π/4) ; sin 45=cos 45=1/√2 and tan 45=1
Sin 60=√3 /2 =Cos 30    and   Cos 60=1/2 =Sin 30

Print the both image by selecting and give a print command to printer and fill the blanks from memory.

Limits Day3

Answers to Exercises in Day 2.

One sided Limits; Example study  Video Extension Video

Limits of trigonometric functions:
1.Review of trignometric ratios and remebering them: Video

Limits Day 2

In the earlier videos and exercises you saw how to find the limits from a graph(plotted readily) with identified undefined values or a different defined value.It was easy to see the approach from below and above a value (say 'a') and declare if the limits were same  if so if it was also the same as f(a).
of the other methods when a graph is not given but a expression (formula of the graph ) is given then  you have to find the limits by algebra...

Video 4.Limits by substitution

Video 5 Limits by factorisation

video 6 Limits by conjugate

Find limits (substitution or by factorisation)
Tip:At times you will find the denominator and the numerator both become "0" on substitution,then you should try factorization. If  by substituting ,for example x=a, results in 0/0,then you know by reminder theorem in algebra,that '(x-a)' must be a factor in numerator and denominator.Using this (x-a) as a factor,you can get the other factors of the Numerator and Denominator.

Day1

A very useful site for Mathematics all topics
Intro to Limits

The topic of limits in calculus is important only upto the stage of start of differential calculus.Thereafter it looses its utility in most of calculus.It appears briefly in definite integrals and thereafter in Series(AP BC) .But the concept is the most important stepping stone for entry into the subject of calculus.The concept of limit is the one that enable one to examine microscopically at the behavior  of functions, which otherwise seem to be just expressions .It enables you to examine as if you are looking at an  atomic particle inside a molecule just by applying simple mathematical tools (learnt in 9th grade level algebra-geometry-trigonometry)

First Blast

Study the videos below-pause and replay if you did not understand some thing-and try to answer the following questions.

You will notice that the video discusses about a function f(x) or may be g(x), and adresses a problem that arises when"x"=some value...

Explain the reason for "the gap".

How does the limt concept overcomes the 'gap problem'?

Limits Intro

First Lessons

Right through the limits chapter and its problems,one fact that can be easily overlooked and make you stumble is that limit is not the same as substituting for 'x' in f(x).....though in some situations  you can find it by substitution. Later you will learn the truth about it and to be watchful.Its for this reason the videos talk about approaching a value and not substituting the value.

Below is Simple intro using a st line function - graph.(DON'Tgo to other videos on the sides-they will come later and will confuse you now)

Video1 limits

You should pay attention to the symbolic way of expressing limit(from left hand side and right hand side)-they can easily confuse you when solving a problem and potential error causing symbols.Try to understand the difference between the approaching a limit value from a negative side and the positive side (I say in my mind -as from below the value and above the value...that reduces  errors).Later you will do lots of problems involving the side of approach.

video 2.Limits in graphs-left hand and right hand limits

Clear all doubts before watching next viseo.Keep a paper pencil for any scratch work.

video 3. Exercises-Limits from graph

Study the problem below and check answers.

Exercise

1. Below is the graph of .  For each of the given points determine the value of , , , and .  If any of the quantities do not exist clearly explain why.

(a)                       (b)                       (c)                       (d)