Intermediate Value Theorem

Mean Value  Theorem

Extreme Value Theorem

Rolles Theorem

1.These are informal explanations for quick recollection of its actions.

Conditions:

2.All functions must be differentiable (so it must also be continuous) to apply these theorems in the open interval  specified. (includes end points)

3.The result of the theorem is applied in the  closed interval [a,b] (that is excludes end points)

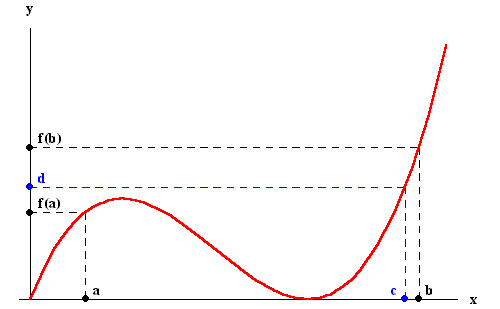
Intermediate Value Theorem:

IVT picture

You can find f(c)=d intermediate between f(a) and f(b)

Mean Value Theorem

For a secant line slope f(b)-f(a)  / (b-a)   you can find at least one  point between 'a' and 'b' where a tangent line is parallel (same slope as secant line) to the secant line .

Rolle Theorem

If f(a)=f(b), then a point 'c' has slope =0 {special case MVT}

Extreme Value Theorem

Between f(a) and f(b) there is a f(c) maximum and f(d) minimum.

Examples of problems:

Here are a few more typical Mean Value Theorem (MVT) problems.  Note that when we get our value of c, we have to make sure it lies in the interval we’re given.

Note also that these problems may be worded something like this:  For what value of c on a certain open interval would the tangent to the graph of a certain function be parallel to the the secant line in that closed interval?

AP problems