Reiman Sums and def imtegrals Khan

Reiman analysis Khan series 1
Reiman analysis Khan series 2
Reiman Khan Trapezoidal rule 3
Reiman sum and definite integrals
Review Reimann

DOMAIN ANALYSIS

Informal Explanations:

All real values of 'x' - infinity to  + infinity that permits a function to exist.

There are only 3 types functions that restrict domains.

1.Functions under a even root radical, or exponent m/n has n only as even  number.
(ex x^1/2; x^3/4;x^5/4--) have to be >=0

domain restriction graph of fractional exponents
you can experiment in the above link apart from study.

2.Functions that have denominators whose 'x' value will make it '0'.
The function is DNE at the 'x' value.(ex 3x-1/3x-2  cannot have x=2/3  f(2/3) is DNE)
Domain of rational functions

3.log f(x) must have f(x) greater than'0'.
 The term of the log ;That is f(x) must be >0.
Ex: log{ (x^3)-7} must be such x^3-7 >0 (be careful to exclude '0')

It is the same rule for all types of bases.Bear in mind that, Base 0 does exist as it is absurd.

Intermediate Value Theorem

Mean Value  Theorem

Extreme Value Theorem

Rolles Theorem

1.These are informal explanations for quick recollection of its actions.

Conditions:

2.All functions must be differentiable (so it must also be continuous) to apply these theorems in the open interval  specified. (includes end points)

3.The result of the theorem is applied in the  closed interval [a,b] (that is excludes end points)

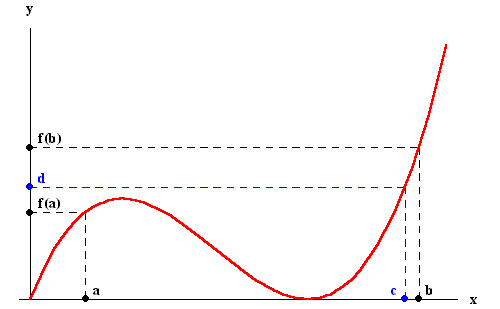
Intermediate Value Theorem:

IVT picture

You can find f(c)=d intermediate between f(a) and f(b)

Mean Value Theorem

For a secant line slope f(b)-f(a)  / (b-a)   you can find at least one  point between 'a' and 'b' where a tangent line is parallel (same slope as secant line) to the secant line .

Rolle Theorem

If f(a)=f(b), then a point 'c' has slope =0 {special case MVT}

Extreme Value Theorem

Between f(a) and f(b) there is a f(c) maximum and f(d) minimum.

Examples of problems:

Here are a few more typical Mean Value Theorem (MVT) problems.  Note that when we get our value of c, we have to make sure it lies in the interval we’re given.

Note also that these problems may be worded something like this:  For what value of c on a certain open interval would the tangent to the graph of a certain function be parallel to the the secant line in that closed interval?

AP problems

MAX MIN CONCAVITY INFLECTION Points

Characteristics of a functions:
max Min point on a graph
Features of a curve of functions Video
Displacement,Velocity acceleration .  school typr problem
Concavity

Answer the following questions based on above :
1.How do you identify the derivative signs at different points on the graph?
2.What features of the slope defines that the curve at a point region is concave down/concave up (cup up/cup down)?
3.What is an inflection point.Where does an inflection point occur in a graph? What is the difference between the slope '0' point (also known as stationary point) and an inflection point.
4.Does the concavity  always alternate like up/down in general or can there be exceptions ?If exceptions are there -them what are they?

Inflection point testing Video tells you some techniques of analysing.
Answer the following.
The video showed a quick way to analyse slopes using signs without drawing the derivative graph.,what was it.Give example.
A note on linkin 1st derivative fraph to f(x)
f '(x) -  to 0 to+ U [smiling f(x) ] ;f'(x) + 0 -  ∩ (Sad f (x))
It also showed how to look for concavity using  signs of 2nd derivative  and the inflection point..describe it.
When can there be no inflection point?
Exercise:
1.Graph the following f(x), fulfilling all conditions:

Domain [-3,3],f(-3)=4,f(3)=1

f(x) increasing on [-3,-1],f(x) decreasing on [-1,1],f’’(x)>0 on [-1,1],f”(x)<0 on [1,3].

Find Abs Max and Min points and inflection points.

State with reasons
2. y=-x^3=3x^2+1 .at which point is the slope Maximum.

 Learning CapsculeBahskara Academy link

Quick Revision:
Limits
1.Quick start
2.Infinite limits graph.
3.Limits from graphs.
4.1.Graphing limits   2.School  exercise